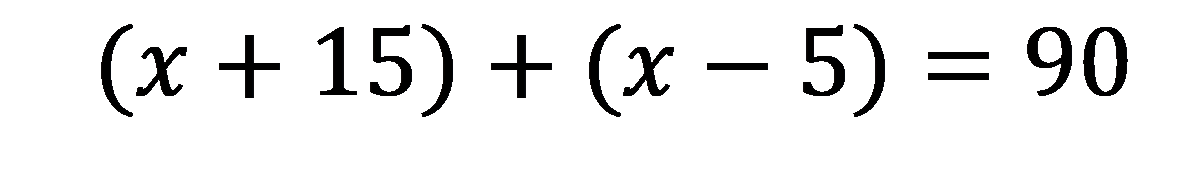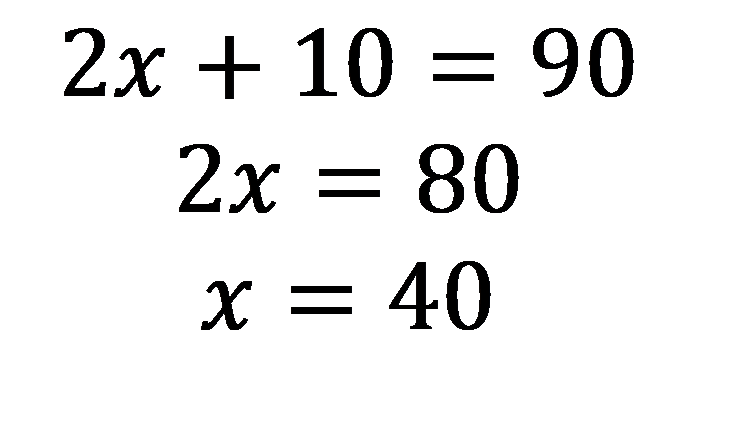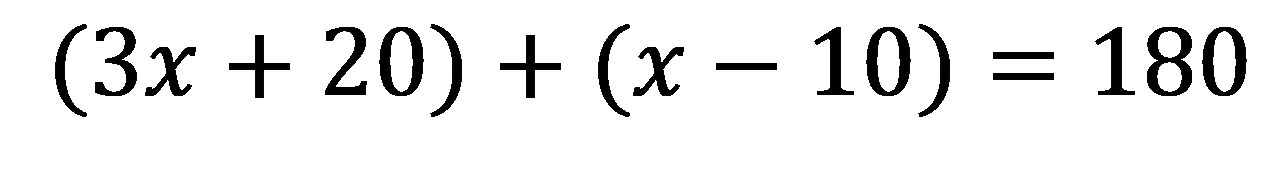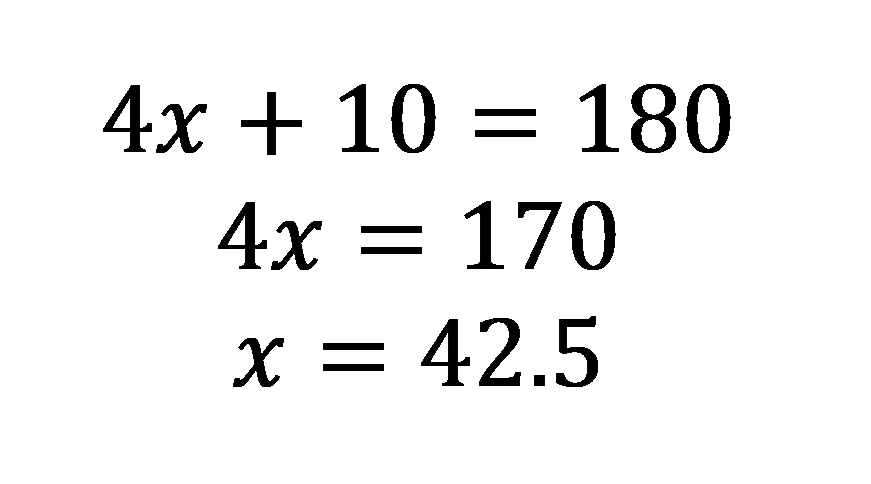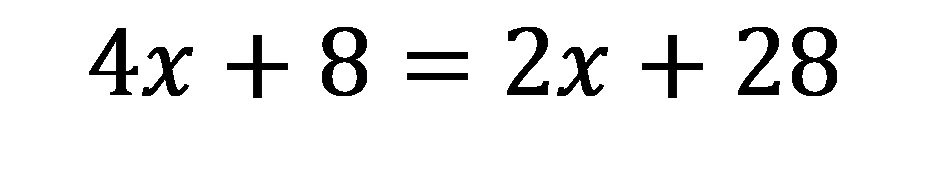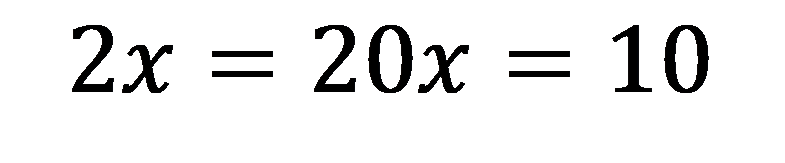Writing Equations for Angle Relationships: Stop Clowning Around
If you’ve ever taught angle relationships, you know the moment.
You introduce complementary, supplementary, and vertical angles… and suddenly students are guessing, adding random numbers, or confidently declaring answers with absolutely no work shown.
This is the point in the unit where the math circus begins.
And while clowns are fun at the fair, they don’t belong in equation writing.
It’s time to stop clowning around and help students learn how to write and solve equations for angle relationships the right way.
Why Angle Relationships Trip Students Up
Angle problems look simple, which is part of the problem.
Students often:
Memorize definitions without understanding them
Add angles that shouldn’t be added
Forget that variables represent unknown measures
Skip the equation writing entirely
Angle relationships are one of the first times students must translate geometry into algebra, and that’s a big leap. If they don’t learn to write equations now, they’ll struggle later with parallel lines, polygons, and Algebra.
Step 1: Complementary Angles — The 90° Rule 🎯
Complementary angles add up to 90 degrees. Simple, right?
Yet students often forget what they’re adding and why.
Example:
Two complementary angles are labeled:
Angle A = X + 15
Angle B = X - 5
Write the equation:
Now solve:
Once x is found, students substitute back to find each angle measure.
Teaching point:
✔ Complementary angles ALWAYS lead to a sum of 90
✔ The equation comes first, not the arithmetic guess
Step 2: Supplementary Angles — The Straight Line Trick 📏
Supplementary angles add up to 180 degrees and often appear on a straight line. This visual helps students tremendously.
Example:
Two angles on a straight line:
Angle 1 = 3x + 20
Angle 2 = x - 10
Write the equation:
Solve:
Students tend to rush these problems, but slowing them down to:
Identify the relationship
Write the equation
Solve carefully
makes a huge difference.
Teaching point:
✔ Supplementary angles = straight line = 180
✔ Diagrams matter—don’t skip them
Step 3: Vertical Angles — Equal Means Equal ✖️
Vertical angles are opposite angles formed by intersecting lines, and they are congruent (equal in measure).
This is where students often overthink.
Example:
Two vertical angles are labeled:
Angle A = 4x + 8
Angle B = 2x + 28
Write the equation:
Solve:
No adding to 90.
No adding to 180.
Just set them equal.
Teaching point:
✔ Vertical angles are equal
✔ If students add them, the clown nose comes out 🤡
The Real Skill: Writing the Equation First
The biggest mistake students make is trying to solve in their head instead of writing an equation.
Angle relationships are less about memorization and more about:
Identifying the relationship
Translating words and diagrams into algebra
Practicing structured problem-solving
When students write equations consistently, confidence replaces guessing.
How to Stop the Clown Show in Your Classroom 🎪
What works:
Lots of targeted practice
Clear diagrams
Problems that force students to write equations
Immediate feedback
What doesn’t:
One worksheet and moving on
Only numeric examples
Letting students skip steps
Angle equations need repetition with purpose—not chaos.
Ready-to-Use Practice That Actually Works
If you want students to stop clowning around and start solving angle equations correctly, this worksheet is designed for exactly that:
👉 Angles in Geometry: Solving Equations Practice Worksheet
Why teachers love it:
Focuses on writing and solving equations
Covers complementary, supplementary, and vertical angles
Middle-school friendly and Algebra-ready
Printable, no-prep, and easy to grade
Builds the exact skills students need for future geometry success
Angle relationships don’t have to feel like a circus act.
With the right structure and practice, students can confidently write equations, solve them, and finally understand what those angles are doing.
🎯 Less guessing.
📐 More reasoning.
🤡 And absolutely no clowning around.